今回は前回に引き続いて結晶構造を扱っていきます.今回は面心立方格子,六方最密構造を扱っていきます.
面心立方格子
面心立方格子は立方体の各面の中心と各頂点に原子が配置した結晶構造のことです.図にすると次のような形です.
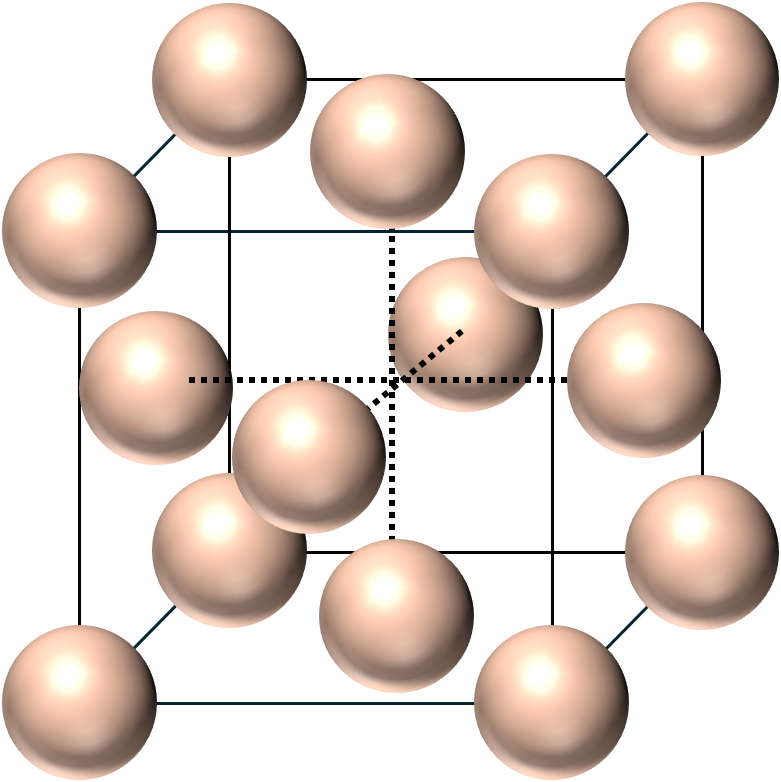
面心立方格子の場合は同一平面上にある原子と最も近くなっており,配位数は12になっています.下の図では2つの単位格子をつなげて描いています.赤い球に注目すると,その周りには青色で示した球が12個あります.これが最近接の粒子になります.

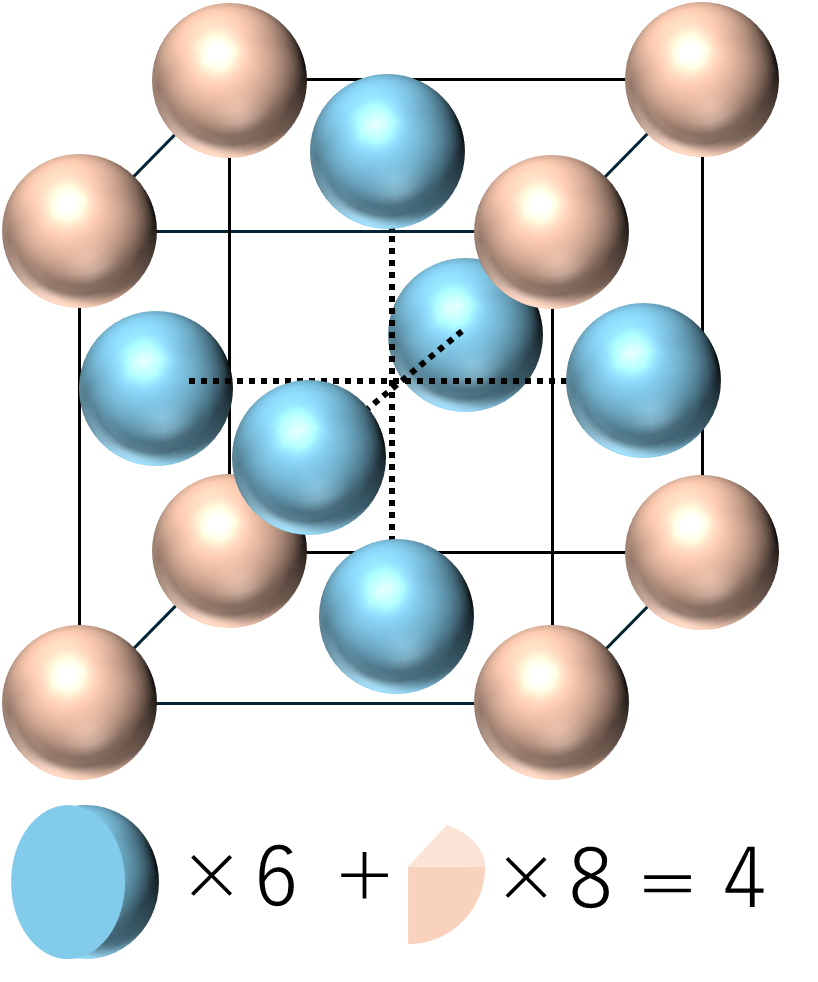
続いて,単位格子中の粒子数を数えましょう.まず,各面の中央に位置した粒子は$\frac{1}{2}$個分の粒子になります.これが単位格子中には合計で6個存在しています.また,各頂点に$\frac{1}{8}$個分の粒子が8個存在しています.よって$\frac{1}{2} \times 6 + \frac{1}{8} \times 8 = 4$となります.したがって単位格子中の原子の数は4個と言うことになります.
では次に充填率を考えましょう.単位格子の1辺の長さを$l$とおきます.このときの立方体の各面は次のようになります.
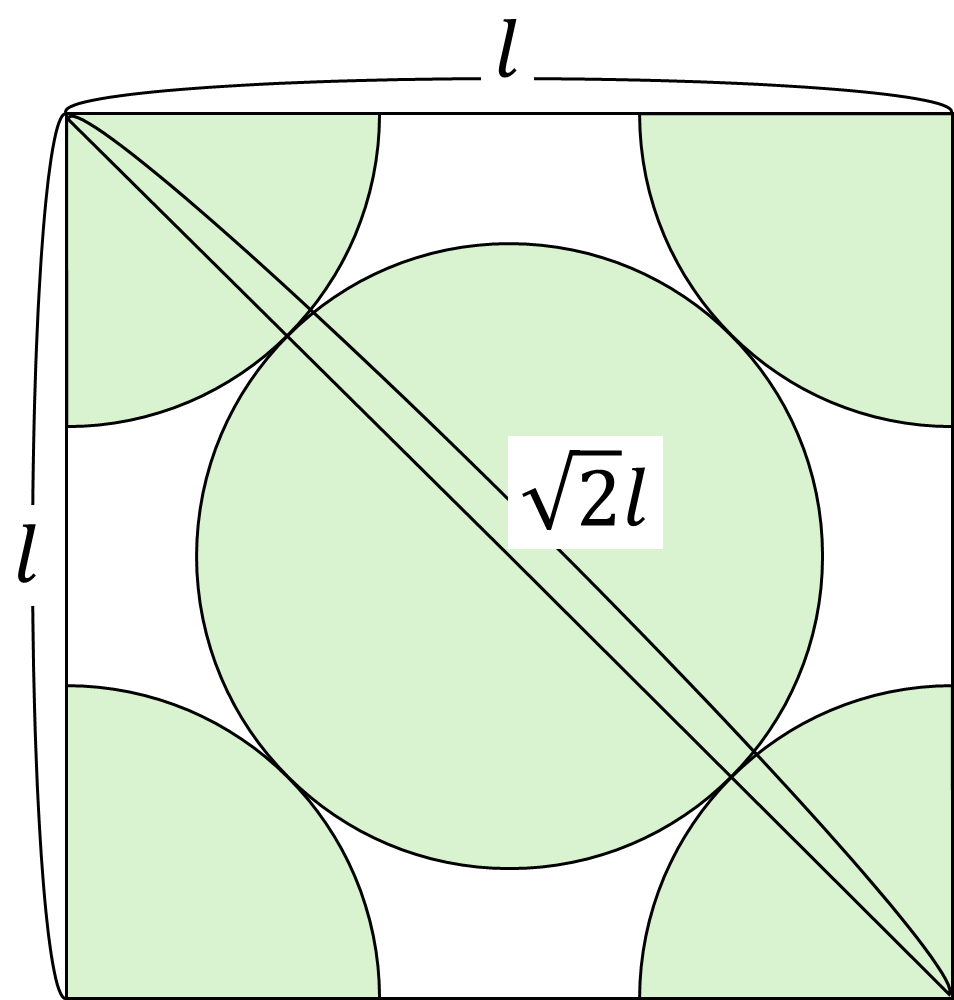
対角線の長さは$\sqrt{2}l$ですので,粒子の半径を$r$とすると$\sqrt{2}l=4r$となります.ゆえに$r=\frac{\sqrt{2}}{4}$です.よって,粒子の体積は次のように求まります.
\begin{eqnarray}
V &=& \frac{4}{3} \pi r^3\\
&=&\frac{4}{3} \pi \Big(\frac{\sqrt{2}l}{4}\Big)^3 \\
&=& \frac{\sqrt{2} \pi}{24}l^3
\end{eqnarray}
面心立方格子の場合,単位格子内に粒子は4つあり,単位格子の体積は$l^3$です.よって
\begin{eqnarray}
\frac{\frac{\sqrt{2} \pi}{24}l^3 \times 24}{l^3} &=& \frac{\sqrt{2}\pi}{6}\\
&\approx& 0.74
\end{eqnarray}
より,74%となります.
以上をまとめると次の通りです.
| 粒子数 | 配位数 | 充填率 |
| 4 | 12 | 74 % |
六方最密構造
最後に六方最密構造をやっていきます.六方最密構造はこれまでの単位格子以上に分かりにくいので頑張ってください.
六方最密構造は次のような配置になっています.
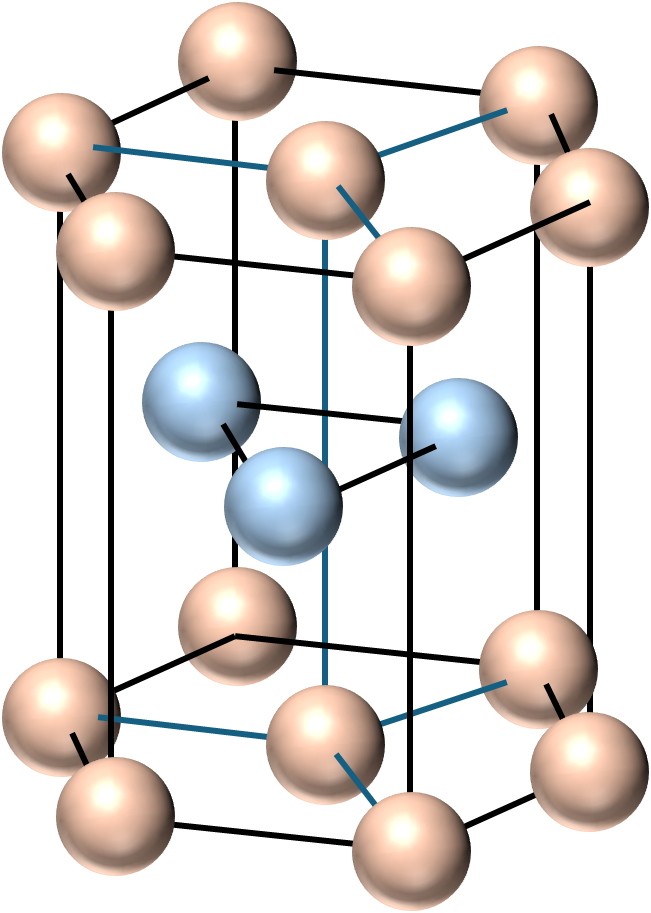
六方最密構造の単位格子はこの正六角柱を3つに分割した際の1つになります.つまり,下の図の緑色の部分になります.
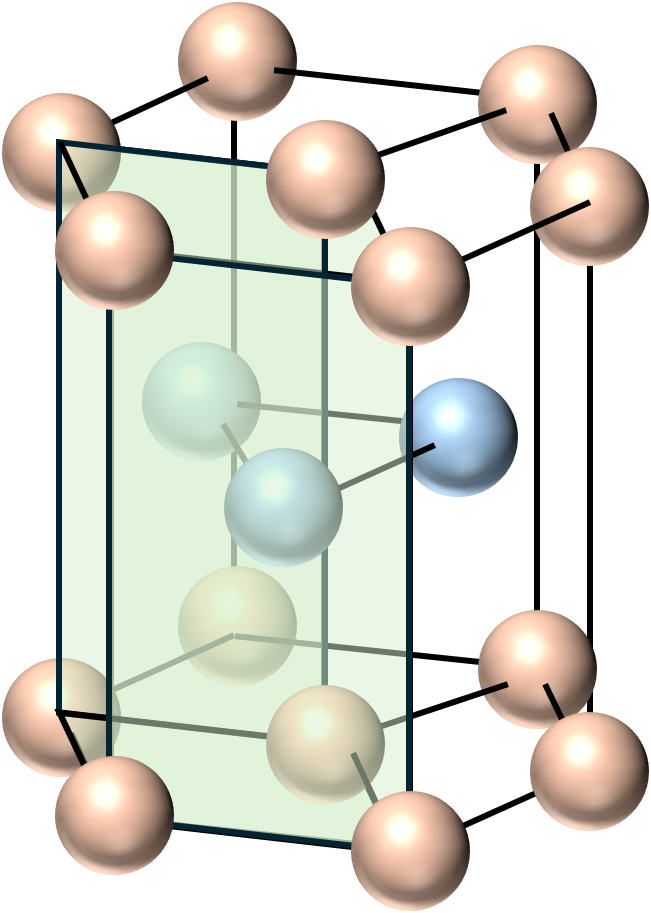
また,六方最密構造における粒子の層の重なり方は次のようになっています.

4つの粒子で正四面体を形成するように重なっています.
では配位数について考えていきましょう.上の図で中央にあるオレンジ色の粒子に注目してみましょう.そうすると,まず同じ層にある6つのオレンジ色の粒子と接しています.加えて上の層にある3つの青い粒子と接しています.この青い粒子はオレンジ色の層の下にもあるので,青い粒子とは合計6つ接しています.よって合計12個の粒子と接しています.ゆえに配位数は12ということになります.
次に単位格子中の粒子の数を数えてみましょう.単位格子で考えるのは少し難しいので,3つの単位格子をあわせた正六角柱の構造を考えましょう.すると粒子全体が含まれているものが3つ,$\frac{1}{2}$個分の粒子が2つ,$\frac{1}{6}$個分の粒子が12個から構成されています.よって,単位格子3つで$3+\frac{1}{2} \times 2 + \frac{1}{6} \times 12 = 6$となります.図にすると次のような形です.
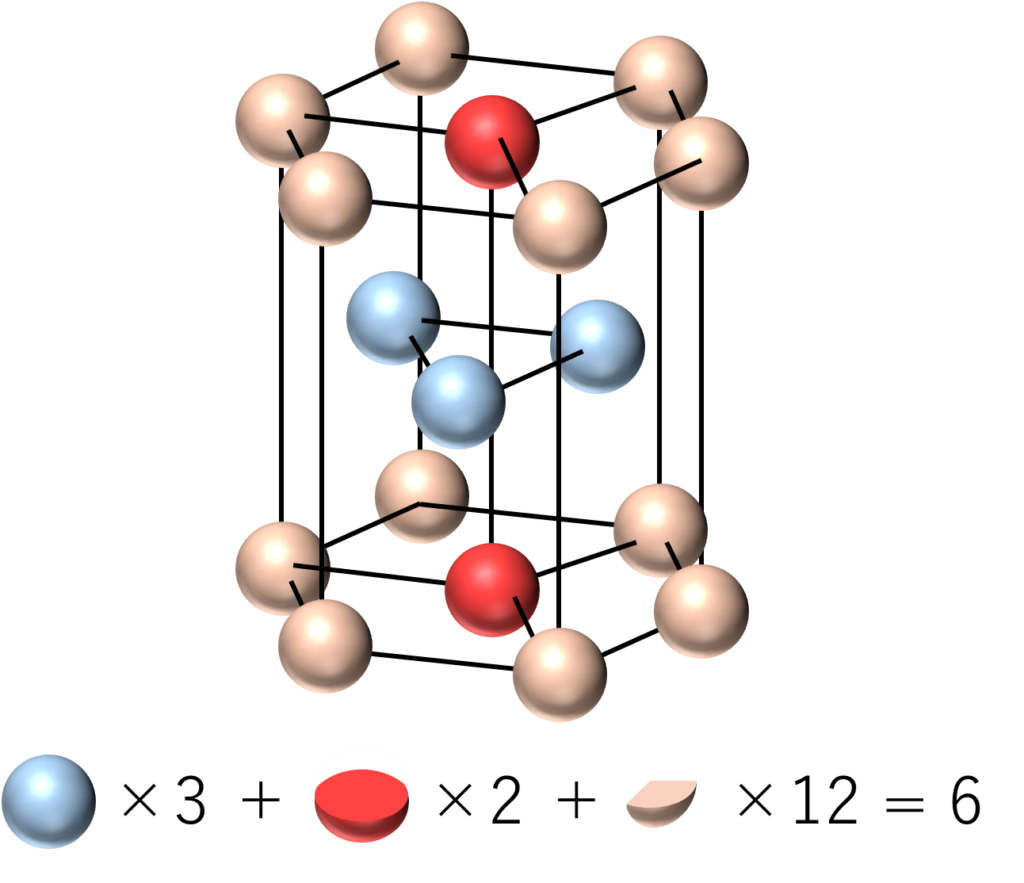
したがって,単位格子3つに粒子が6つ含まれるため,単位格子1つだと2つということになります.
最後に充填率を考えます.先ほど1層目と2層目の粒子は4つの粒子で正四面体を形成するように重なっていると書きました.そこでまずは正四面体について考えていきます.正四面体の1辺の長さを$l$とすると,各部分の長さは次のようになります.
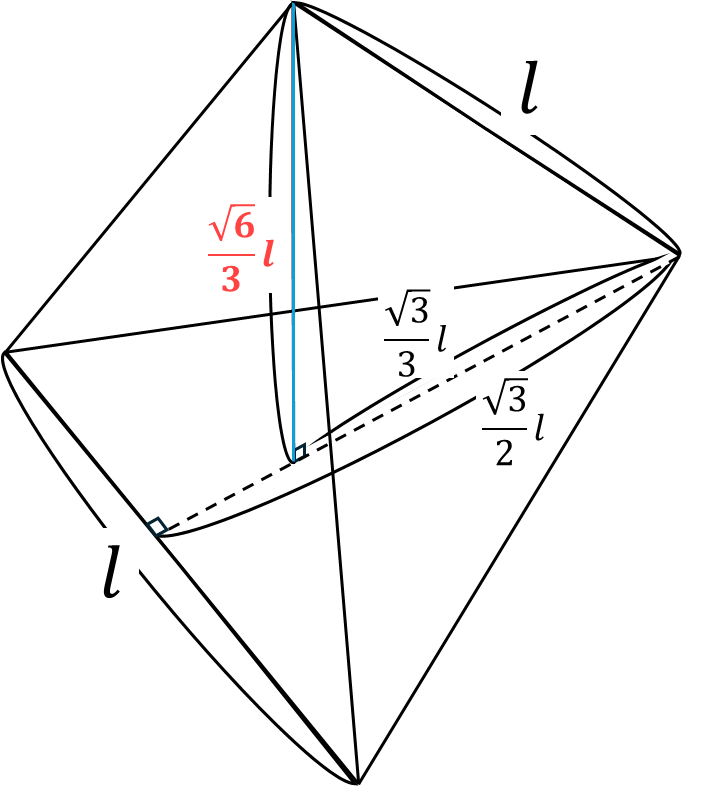
これらの線の長さは重心の比や三平方の定理から求まります.正四面体の高さは$\frac{\sqrt{6}}{3}l$となります.この値は単位格子の1層目と2層目の高さと等しくなります.よって,単位格子の高さはこの値の2倍になります.ゆえに単位格子の各辺の長さは次のように書けます.
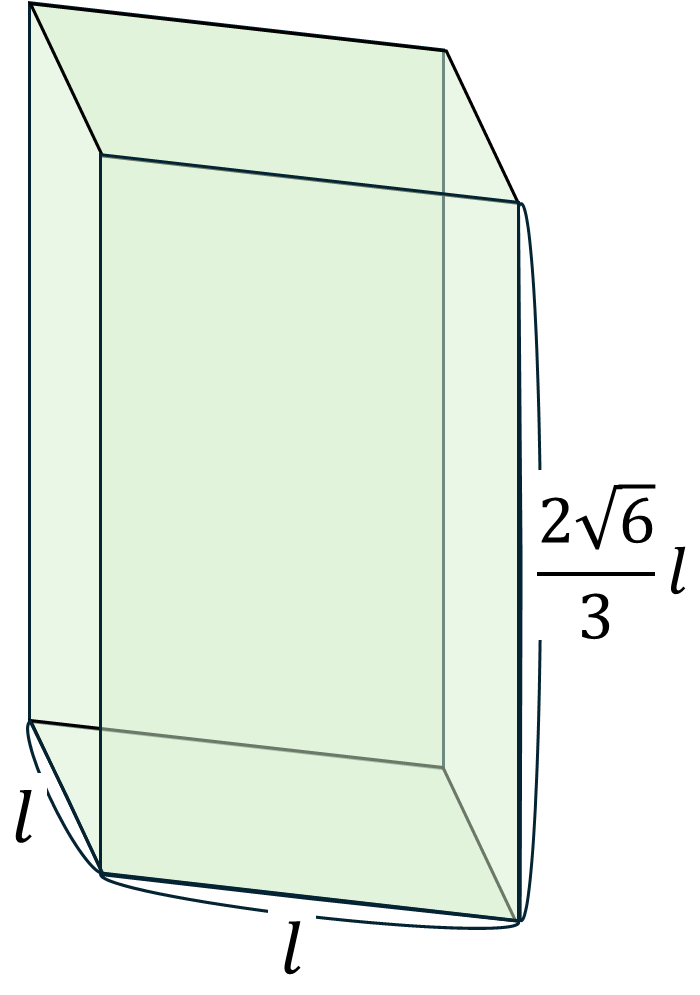
したがって,単位格子の体積は次のように計算できます.
\begin{eqnarray}
V &=& \frac{1}{2} l \cdot l \sin{\frac{1}{3}\pi} \times 2 \times \frac{2\sqrt{6}}{3}l\\
&=&\sqrt{2}l^3
\end{eqnarray}
粒子の半径$r$は$\frac{1}{2}l$と書けます.よって,粒子の体積は次のように計算できます.
\begin{eqnarray}
V’ &=& \frac{4}{3} \pi r^3\\
&=&\frac{4}{3} \pi \Big( \frac{1}{2}l \Big)^3 \\
&=& \frac{\pi}{6}l^3
\end{eqnarray}
六方最密構造には粒子が2つ含まれるため充填率は以上の値を用いて
\begin{eqnarray}
\frac{2V’}{V} &=& \frac{2 \times \frac{\pi}{6}l^3}{\sqrt{2}l^3 } \\
&=& \frac{\sqrt{2}\pi}{6} \\
&\approx& 0.74
\end{eqnarray}
と求まります.ゆえに,六方最密構造の充填率は74%となります.
以上をまとめると次の通りです.
| 粒子数 | 配位数 | 充填率 |
| 2 | 12 | 74 % |
まとめ
ここまで2回にわたって結晶構造について解説してきました.原子や分子などには規則的に配列した結晶と呼ばれるものと,規則性がない非晶質と呼ばれるものがあります.結晶の配列にはいくつか種類があり,体心立方格子,面心立方格子,六方最密構造などがあります.これら3つの配位数,単位格子中の粒子数,充填率は次の通りになります.
| 配位数 | 粒子数 | 充填率 | |
| 体心立方格子 | 8 | 2 | 68 % |
| 面心立方格子 | 12 | 4 | 74 % |
| 六方最密構造 | 12 | 2 | 74 % |
今回の内容でご不明な点がございましたらお気軽にお問い合わせください.



コメント