ここでは,物質の結晶構造について解説していきます.
結晶
結晶とは原子や分子などが規則的に配列した固体のことです.この規則的な配列にはいくつかの種類があります.結晶は一定の融点を持っています.一方で,規則的な配列を持たない固体を非晶質(アモルファス)と呼びます.
今回はこのうち結晶について解説します.結晶がもつ規則的な構造は結晶格子と呼ばれ,その最小単位を単位格子と呼びます.つまり,単位格子が複数集まった状態が結晶格子ということになります.
この単位格子にはいくつかの種類があります.その中でも代表的なものが体心立方格子,面心立方格子,六方最密構造です.今回はこのうち体心立方格子を扱っていきます.面心立方格子,六方最密構造については次の記事をお読みください.
単位格子
体心立方格子
まずは体心立方格子について説明します.体心立方格子とは立方体の中心と8つの頂点上に原子が配置した結晶構造のことです.図にすると次のような形です.
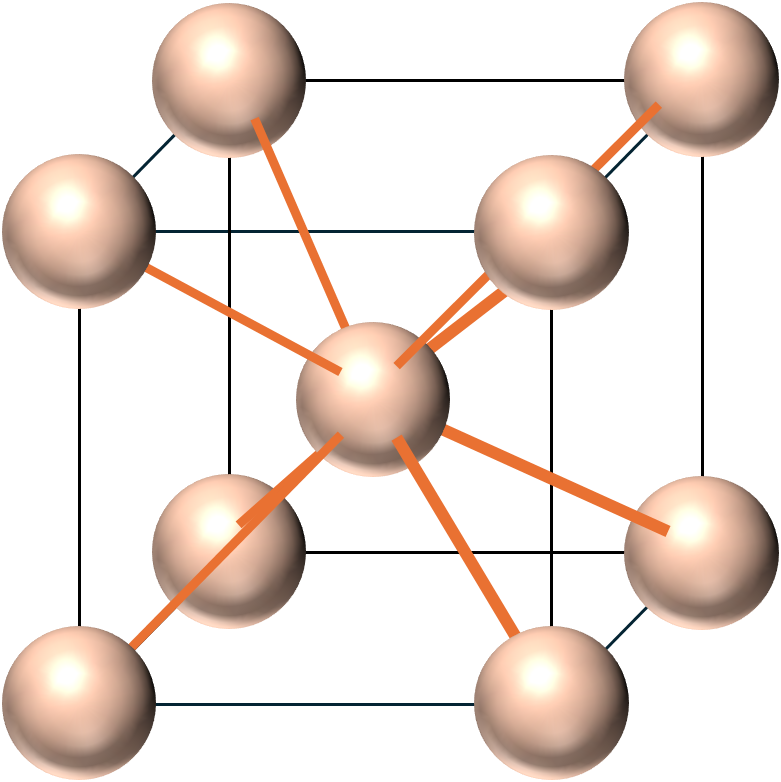
単位格子を考える上で重要な値が単位格子中の原子の数と配位数,充填率があります.
単位格子中の原子の数とはその名の通り,1つの単位格子に含まれている原子の数のことです.体心立方格子の場合は中央に原子が1つ,8つの頂点上に原子の$\frac{1}{8}$個分が含まれています.よって,$1 + \frac{1}{8} \times 8 = 2$個ということになります.
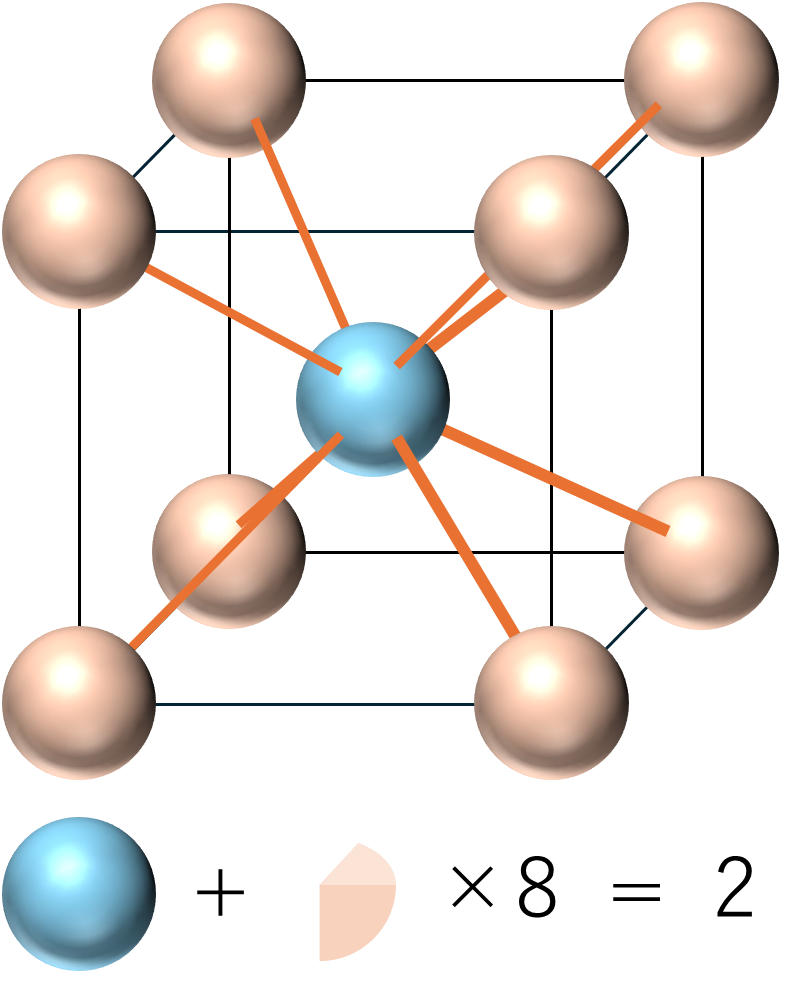
続いて配位数です.配位数とは最も近くに存在している粒子の数のことです.今回は中央の粒子に注目してみましょう.この粒子の最も近くに存在しているのは立方体の頂点上にある粒子です.よって配位数は6になります.
次に充填率です.単位格子には原子がらなっている部分の他に若干の隙間もできています.充填率とは単位格子のうち粒子が占める割合のことです.充填率が大きいほど隙間が少ない構造ということになります.では,体心立方格子の充填率を計算してみましょう.
単位格子の1辺の長さが$l$である場合を考えます.このときに粒子の半径がいくつになるかを求めます.
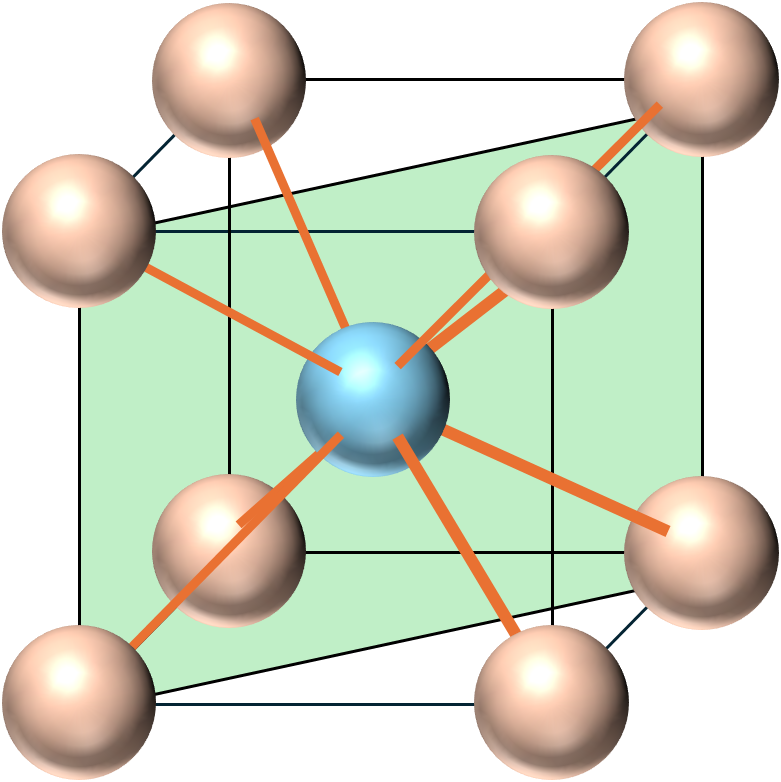
図のような斜めの面で切断した平面を考えましょう.このときの断面は次のようになります.
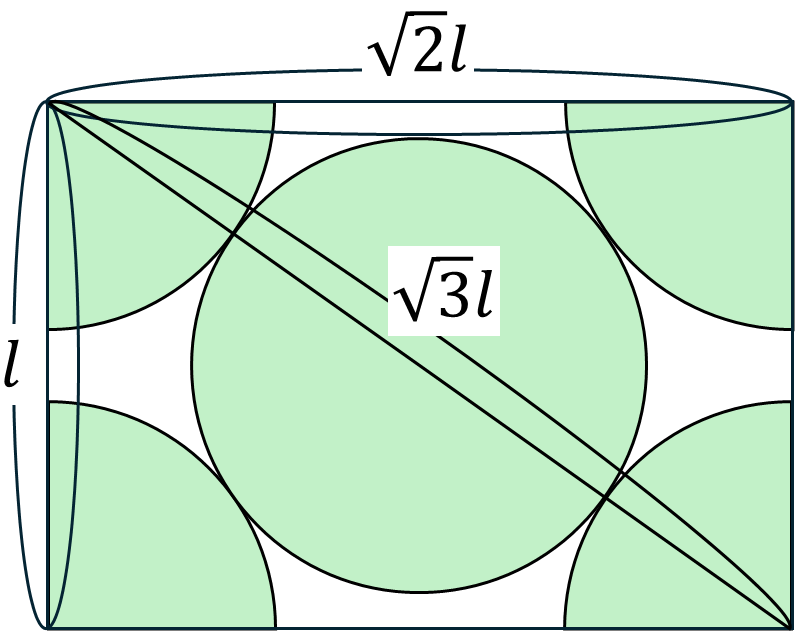
断面は縦$l$,横$\sqrt{2}l$,対角線$\sqrt{3}l$の長方形になります.粒子の半径を$r$とすると$\sqrt{3}l=4r$となるため,$r=\frac{\sqrt{3}l}{4}$です.ゆえに粒子の体積は次のように計算できます.
\begin{eqnarray}
V &=& \frac{4}{3} \pi r^3\\
&=&\frac{4}{3} \pi \Big(\frac{\sqrt{3}l}{4}\Big)^3 \\
&=& \frac{\sqrt{3} \pi}{16}l^3
\end{eqnarray}
体心立方格子の場合,単位格子内に粒子は2つあり,単位格子の体積は$l^3$です.よって
\begin{eqnarray}
\frac{\frac{\sqrt{3} \pi}{16}l^3 \times 2 }{l^3} &=& \frac{\sqrt{3}\pi}{8}\\
&\approx& 0.68
\end{eqnarray}
より,68%となります.
以上をまとめると次の通りです.
| 粒子数 | 配位数 | 充填率 |
| 2 | 8 | 68 % |
密度の計算
この単位格子から物質の密度を求めることができます.この体心立方格子をとる物質として鉄があります.この鉄の密度を考えてみましょう.
先ほどの計算で原子半径は$r=\frac{\sqrt{3}l}{4}$と書けました.これを$l$について解くと$l=\frac{4r}{\sqrt{3}}$と書けます.ゆえに単位格子の体積は$V=\frac{64r^3}{3\sqrt{3}}$となります.
ここでアボガドロ定数$N_A$は1molあたりの粒子の個数,モル質量$M$は1molあたりの質量でした.つまり,1molの粒子があったとき,粒子の個数は$N_A$個であり,質量は$M$です.よって,1つの粒子の質量は$\frac{M}{N_A}$となります.体心立方格子の場合,1つの単位格子に粒子は2つ含まれるため,単位格子1つの質量は$\frac{2M}{N_A}$となります.
以上より,単位格子の体積は$\frac{64r^3}{3\sqrt{3}}$,質量は$\frac{2M}{N_A}$です.鉄原子の原子半径は124pm(=$1.24 \times 10^{-8}$cm),原子量は55.8,アボガドロ定数は$6.02 \times 10^{23}$とします.これを用いると次のように計算できます.
\begin{eqnarray}
d &=& \frac{\frac{2M}{N_A}}{\frac{64r^3}{3\sqrt{3}}}\\
&=&\frac{6\sqrt{3}M}{64r^3N_A} \\
&=& \frac{6\sqrt{3} \times 55.8}{64 \times (1.24 \times 10^{-8})^3 \times 6.02 \times 10^{23}}\\
&=& 7.89
\end{eqnarray}
よって7.89g/cm3と求まります.
まとめ
以上で結晶構造①を終わりたいと思います.
原子や分子などの粒子が規則的に配列しているものを結晶,規則的に配列していないものを非晶質と呼びました.結晶の規則的な構造を結晶格子と呼び,その最小単位を単位格子と呼びます.その単位格子には体心立方格子や面心立方格子,六方最密構造などの種類があります.その単位格子を考える上で重要なのが配位数や単位格子中の原子数,充填率です.
今回は体心立方格子と中心に扱いました.次回は面心立方格子,六方最密構造を扱いますので,是非お読みください.今回の内容でご不明な点がございましたらお気軽にお問い合わせください.



コメント