今回はボイル・シャルルの法則,気体の状態方程式の証明をしていきます.
ボイルの法則
下の図の様な一辺の長さが$l$の立方体を考えます.この中に質量$m$の原子が$N$個,速度$v$で移動しているとします.このとき,原子の速度の$x$成分を$v_x$とします.
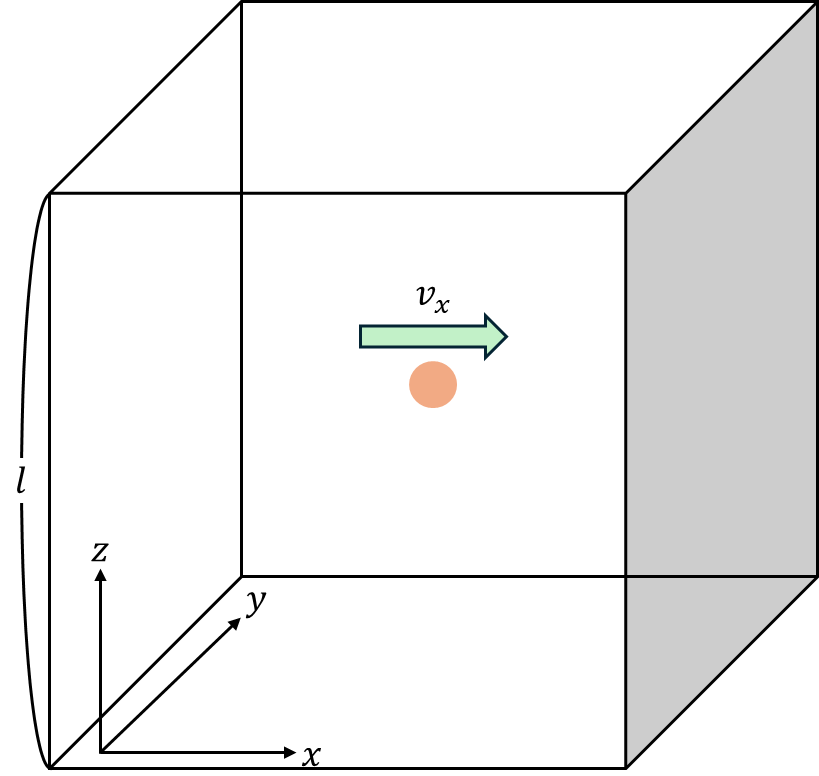
まずは1つの原子の$x$方向の動きに注目していきます.原子が端から端までを往復するのにかかる時間を$\Delta t$とすると,速度$v_x$で距離$2l$を移動するので$\Delta t = \frac{2l}{v_x}$と書けます.この$\Delta t$の間に図の灰色の面に1回衝突します.
ここで灰色の面に衝突した際の運動量変化量を考えます.この面における衝突が弾性衝突である場合,運動量は$mv_x$から$-mv_x$に変化します.ゆえに運動量変化量は$2mv_x$となります.
ここで$f \Delta t = (運動量変化)$という関係が成り立ちます.$f$とは壁が受ける力のことです.この式に$\Delta t = \frac{2l}{v_x}$と$2mv_x$を代入すると
\begin{eqnarray}
f \Delta t &=&2mv_x\\
f \frac{2l}{v_x} &=&2mv_x\\
f &=& \frac{m{v_x}^2}{l}
\end{eqnarray}
となります.
今回考えている箱の中には$n$個の原子が存在しています.そのため,壁が受ける力は$n$個の原子それぞれが与える力の総和になります.ゆえに,この壁が受けるの力総和を$F$とすると次のように書けます.
$$F = \sum_{i=1}^{N} \frac{m v_{xi}^2}{L} = \frac{m}{L} \sum_{i=1}^{N} v_{xi}^2$$
${v_x}^2$の平均を$\overline{v_x^2}$とすると,$\sum_{i=1}^{N} v_{xi}^2 = N\overline{v_x^2}$となります.ただし,$\overline{v_x^2}$は${v_x}^2$の平均であって,$v_x$の平均の2乗ではないので注意してください.
さらに,原子の運動は完全にランダムであるため,方向によってその偏りは生じません.ゆえに$\overline{v_x^2} = \overline{v_y^2} = \overline{v_z^2} $と書けます.また,$x$,$y$,$z$方向の運動量をすべて加えると,全体の運動量になるはずであるため次のように計算できます.
\begin{eqnarray}
\frac{1}{2}m\overline{v_x^2} + \frac{1}{2}m\overline{v_y^2} + \frac{1}{2}m\overline{v_z^2} &=&\frac{1}{2}m\overline{v^2}\\
\frac{1}{2}m\overline{v_x^2} + \frac{1}{2}m\overline{v_x^2} + \frac{1}{2}m\overline{v_x^2} &=&\frac{1}{2}m\overline{v^2}\\
\frac{3}{2}m\overline{v_x^2} &=&\frac{1}{2}m\overline{v^2}\\
\overline{v_x^2}&=&\frac{1}{3}\overline{v^2}
\end{eqnarray}
以上より
\begin{eqnarray}
F &=& \frac{m}{l} \sum_{i=1}^{N} v_{xi}^2\\
&=& \frac{m}{l} N\overline{v_x^2} \\
&=& \frac{m}{l} N \frac{1}{3}\overline{v^2} \\
&=& \frac{mN\overline{v^2}}{3l}
\end{eqnarray}
となります.灰色の部分の面の面積は$l^2$ですので,この面に加わる圧力$P$は
$$P=\frac{F}{l^2}=\frac{mN\overline{v^2}}{3l^3}$$
となります.
今回考えた箱の体積を$V$とすると$V=l^3$なので,この式は
$$PV=\frac{1}{3}mN\overline{v^2}$$
となりました.箱の中の分子の数や温度が変化しないとき,この式の右辺は変化しないので定数とみなすことができ$PV=k$と書くことができます.よってボイルの法則が導けました.
シャルルの法則
今度はシャルルの法則の式を作っていきます.
先ほどボイルの法則の証明で次の式が導けました.
$$PV=\frac{1}{3}mN\overline{v^2}$$
この式を少し変形すると次のように計算できます.
\begin{eqnarray}
PV &=& \frac{1}{3}mN\overline{v^2}\\
&=& \frac{2}{3}N \times \frac{1}{2}m\overline{v^2}
\end{eqnarray}
ここで$\frac{1}{2}m\overline{v^2}$とは運動エネルギーのことです.この運動エネルギーは温度との関係で次の式が成り立ちます.
$$\frac{1}{2}m\overline{v^2}=\frac{3}{2}k_BT$$
ただし,$k_B$とはボルマン定数と呼ばれる定数です.この式を先ほどの式に代入すると
\begin{eqnarray}
PV &=& \frac{2}{3}N \times \frac{1}{2}m\overline{v^2}\\
&=& \frac{2}{3}N \times \frac{3}{2}k_BT \\
&=& Nk_BT
\frac{PV}{T} = Nk_B
\end{eqnarray}
となります.分子の数が変化しないとき$Nk_B$は一定ですので$\frac{PV}{T} = k’$と書けてボイル・シャルルの法則が導けました.圧力が一定のときは$\frac{V}{T}=k”$とシャルルの法則の形にすることもできます.以上のようにしてシャルルの法則が導けました.
気体の状態方程式
では,最後に気体の状態方程式をやっていきましょう.先ほど求めた式を改めて書いておきます.
$$\frac{PV}{T} = Nk_B$$
分子が$N$とあるとき,これを物質量$n$に変換するとアボガドロ定数を用いて$n=\frac{N}{N_A}$と書けます.ゆえに箱の中には$\frac{N}{N_A}$molの分子が存在することになります.ここで,アボガドロ定数,ボルツマン定数,気体定数には$k_B = \frac{R}{N_A}$という関係が成り立っています.これらを用いると次のように計算できます.
\begin{eqnarray}
PV &=& Nk_BT\\
&=& nN_A \frac{R}{N_A} T\\
&=& nRT
\end{eqnarray}
となります.よって気体の状態方程式が導けました.
ここで,今回証明した法則などは実際には理想気体と呼ばれるものにだけ適用できます.理想気体とは分子の体積や分子間力などを無視した気体のことです.一方で,現実に存在する気体は体積や分子間力を持っています.このような実際に存在する気体のことは実在気体と呼びます.
では,今回の証明ではどのような点を無視していたでしょうか.もし,分子が体積を持っていた場合,必ず分子同士の衝突が起こるはずです.ですが今回は一切分子同士の衝突を考えていませんでした.衝突が起これば$\Delta t$で原子が往復することはできないはずです.
また,分身力が存在していれば全ての分子が完全に自由に動き回ることはできません.そうなると3つの軸方向の運動が全て等価であると考えても良いのでしょうか.
このように今回の証明には少しおかしな点が存在していたのです.では実在気体で当てはまる式がないのかというとそういうわけではありません.実在気体ではファンデルワールスの状態方程式というものが使われます.この式は次のように書けます.
$$\Big(P+\frac{n^2a}{V^2}\Big)(V-na)=nRT$$
式中の$a$や$b$は実験より求められた物質固有の定数です.実在気体の場合はこの式で計算することができます.
まとめ
以上,ボイル・シャルルの法則,気体の状態方程式の証明でした.これらの式は分子の体積や分子間力を無視した理想気体にのみ適用できる仮定のもとに導かれていました.
今回の内容でご不明な点がございましたらお気軽にお問い合わせください.



コメント